Michelson Interferometers, Modulations, and Transfer Functions - Homework 03

This is the third homework assignment for Lasers and Optomechanics at Syracuse University.
It is due Monday, March 02, 2026 by 5 pm

You will need to complete the questions in this jupyter notebook and submit it via gitlab

1Homodyne Michelson¶

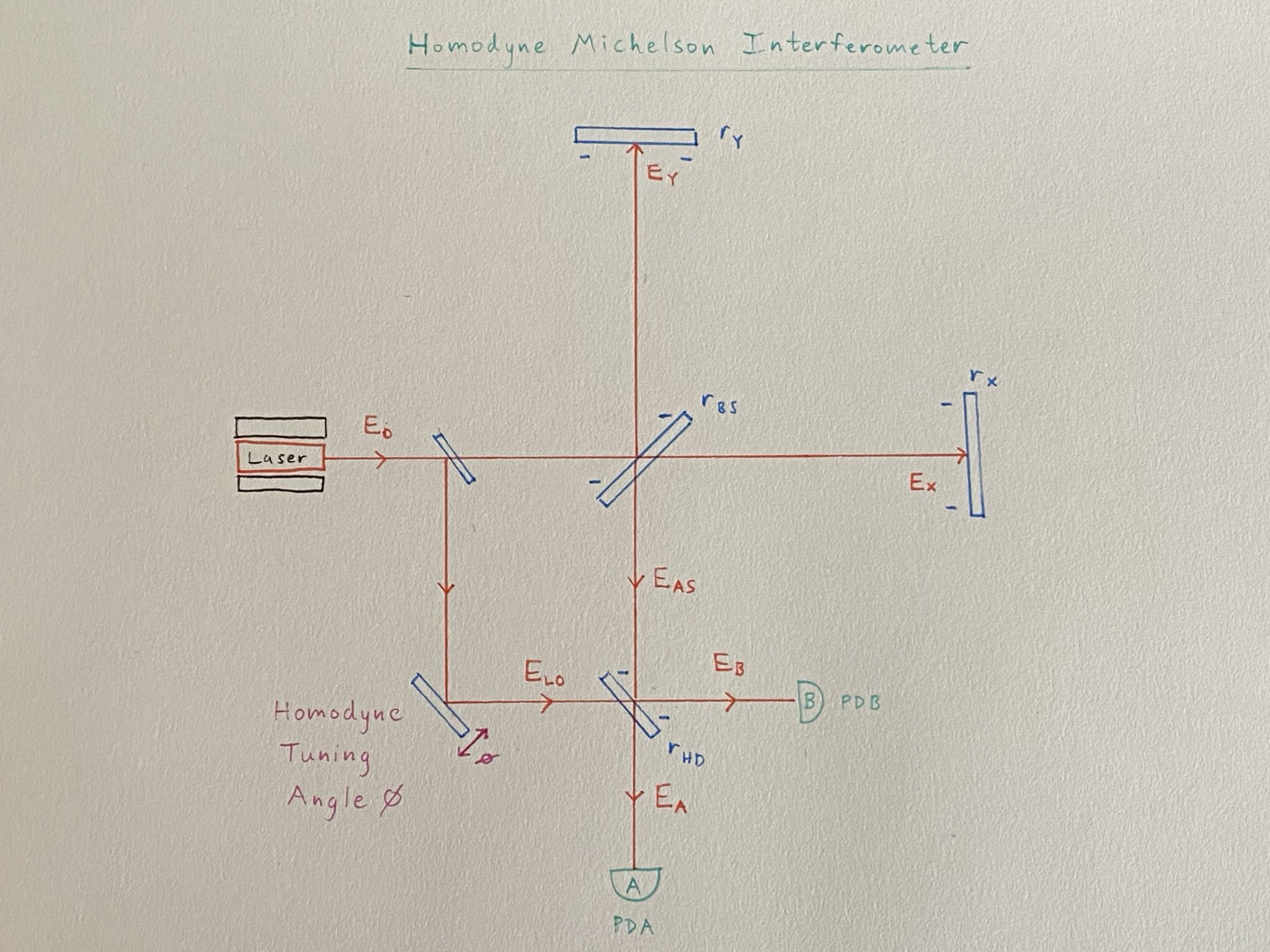
Homodyne Michelson Interferometer Diagram

1.1Adjacency Matrix¶

Set up an Adjacency Matrix $\boldsymbol{M}$ for the Homodyne Michelson.
You may choose any electric fields vector you want, but you have to include the explicitly labeled electric fields.
The homodyne angle $\phi_\mathrm{HD}$ can be considered as the total phase accrued by the local oscillator field $E_\mathrm{LO}$ in the pick-off path:

1.2Electric Field Transfer Functions¶

Invert your Adjacency Matrix minus the identity $(\boldsymbol{M} - \boldsymbol{I})^{-1}$ to calculate the transfer functions from each electric field to every other electric field.
Pick out the field transfer functions from the input to the photodetectors $\mathrm{PD}_A$ and $\mathrm{PD}_B$ $\dfrac{E_\mathrm{PDA}}{E_\mathrm{in}}$ and $\dfrac{E_\mathrm{PDB}}{E_\mathrm{in}}$.

1.3Substitutions¶

Apply the phase change of basis used in class $\phi_d = \dfrac{\phi_x - \phi_y}{2}$ and $\phi_c = \dfrac{\phi_x - \phi_y}{2}$ to your field transfer functions above.
You may also assume a perfect Michelson beamsplitter $r_\mathrm{BS} = t_\mathrm{BS} = \dfrac{1}{\sqrt{2}}$.

1.4Power Transfer Functions¶

Calculate the input to power transfer functions $\dfrac{P_\mathrm{PDA}}{P_\mathrm{in}}$ and $\dfrac{P_\mathrm{PDB}}{P_\mathrm{in}}$.

1.5Interpretation¶

How do $\dfrac{P_\mathrm{PDA}}{P_\mathrm{in}}$ and $\dfrac{P_\mathrm{PDB}}{P_\mathrm{in}}$ depend on the homodyne angle $\phi_\mathrm{HD}$, and the common and differential Michelson phase $\phi_d$ and $\phi_c$?
Can we manipulate the homodyne angle $\phi_\mathrm{HD}$ to detect the differential phase $\phi_d$?
Can you think of any problems you might run into if you tried to actually set up a homodyned Michelson?

2Asymmetric Michelson¶

Suppose you have a Michelson interferometer with the X-arm much longer than the Y-arm:

In this problem, we will calculate the full frequency response transfer functions of the Michelson

I recommend using an algebra helper like Mathematica or sympy for this problem. You may convert your answers to LaTeX using TeXform in Mathematica or some such similar function for sympy.

2.1Field tranfer functions¶

Derive the electric field transfer functions for the following:

where $E_\mathrm{in}$ is the input electric field $E_0 e^{i \omega_0 t}$,
$E_\mathrm{x}$ is the field reflected from the X-arm mirror,
$E_\mathrm{y}$ is the field reflected from the Y-arm mirror,
and $E_\mathrm{as}$ is the field at the antisymmetric (or transmission) port.

Use $r_\mathrm{bs}, t_\mathrm{bs}$ for the beamsplitter reflection and transmission,
$r_\mathrm{x}, r_\mathrm{y}$ for the X and Y mirror reflections, and
$\phi_x, \phi_y$ for the single-pass phase accrued by the field as it propagates in the X-arm or Y-arm.

2.2End Mirror Modulation¶

Now, suppose we apply some common modulation to both end mirrors:

Write what the new arm reflected transfer functions are for:

Hint: Remember that you should end up with three distinct fields at $\omega_0$ and $\omega_0 \pm \omega$

2.3Propagate to the antisymmetric port¶

Propagate your new transfer functions to the antisymmetric port, and compute a new $\dfrac{E_\mathrm{as}}{E_\mathrm{in}}$.

Be careful here.
Consider carefully what $k = \omega/c$ is for each of your electric fields as they propagate back to the beamsplitter, accruing some phase $\phi = -k L$.
Should each field accrue the same phase?

2.4Calculate the power response¶

Calculate the power response to the common motion $\dfrac{P_\mathrm{as}}{P_\mathrm{in}}$.

This is a lot of algebra, I recommend Mathematica or sympy to help you make sure you get things right here.
You may find it useful to express your arm phases in the common and differential bases again, since you have already incorporated the time-dependent term $\Gamma \cos(\omega t)$ as two additional sideband terms:

You may assume an ideal beamsplitter

and balanced arms

and small modulation from the end mirrors

Answer:

2.5Demodulate the power term¶

Calculate

by integrating $P_\mathrm{as}$ over one cycle of $\omega t$ while multiplying by $1, \cos(\omega t)$ and $\sin(\omega t)$, respectively.

Does your answer for $P_\mathrm{as}^\mathrm{DC}$ seem familiar?

2.6Caluculate the Frequency Response to CARM motion in an Asymmetric Michelson¶

Calculate the frequency response

to CARM motion $\Gamma$.

Plot the magnitude and phase for $\dfrac{P_\mathrm{as}}{\Gamma}(\omega)$.

Assume